
a 31-note-per-octave keyboard with pressure sensitive keys

a 31-note-per-octave keyboard with pressure sensitive keys
Modern music is mostly composed, performed, taught, and understood in terms of a tuning system known as 12-tone equal temperament (12-TET), in which an octave (or doubling of frequency) is divided up into 12 logarithmically-equal steps, with each note in the scale having a frequency that's the twelvth root of two times faster than the note below it.
There are many things to like about 12-TET; musical instruments are relatively simple to build and compatible with each other, and performers are free to play in any key and even to modulate from one key to another in the middle of a song.
12-TET is a compromise, though. Certain musical intervals (particularly major and minor thirds and major and minor sixths) are significantly out of tune, resulting in chords that don't sound quite as harmonious as they might. Also, it lacks the ability to make subtle distinctions between notes which are almost but not exactly the same, or the ability to represent those notes which simply fall too far in between two of the 12 notes to be usable.
12-TET was preceded by another tuning system called just intonation (JI), in which the frequencies of all the notes in a scale have whole number ratio relationships with each other. For instance, if the root of the scale (which we call 1/1) is 100 hz, then the major third of the scale (which is known by the ratio 5/4) would be 125 hz exactly. The perfect fifth (3/2) would be 150 hz. Between the fifth and the major third is another implied interval of 3/2 divided by 5/4 (or, alternatively, 150 divided by 125), which is 12/10 according to standard fraction arithmatic and simplifies to 6/5, the minor third. So, whereas in 12-TET terminology we might say that stacking a minor third (3 semitones) on top of a major third (4 semitones) yields a perfect fifth interval of 7 semitones, in JI we would say that stacking a minor third (6/5) on a major third (5/4) is 5/4 times 6/5, which is the perfect fifth interval of 3/2. The same general musical principle applies in both systems, but the actual sizes of the intervals are different.
JI works because most musical tones produce harmonics that are whole-number multiples of their fundamental frequency. So, in our example, the sixth harmonic of 1/1 would be 100 * 6 = 600 hz, the fifth harmonic of 5/4 is 125 * 5 = 600 hz, and the fourth harmonic of 3/2 is 150 * 4 = 600 hz. The harmonics all line up in a way that is pleasing to our ears. If any of those notes were a little off, the difference would arise as a warbly beat frequency, which would sound somewhat objectionable and "out of tune". The absensce of any (slow) beat frequencies allows JI to sound very clean and stable.
There is a long-standing debate between proponents of JI and 12-TET that goes back centuries, and it's not my intention in this article to convince the sceptical reader that they should abandon equal tempered music in favor of JI. Suffice to say both systems are musically useful and capable of expressing great music, but JI especially excells at clarity. Sometimes nothing but a pure chord will do, but those who love the precision of JI are severely constrained by a lack of instruments capable of playing in JI. Most JI music tends to be performed on continuous-pitch instruments like violins, slide guitar, trombones, or the human voice. I would like to see a greater proliferation of fixed-pitch JI instruments, and what follows is meant to describe a means to that end.
I have previously adapted guitars and guitar-like instruments to JI tunings by modifying the layout of frets on the fingerboard. For the most part it works well, but guitars present some difficulties.
In JI, since there are infinitely many whole-number ratios, there are an infinite number of potential notes to choose from. Consequently, those who build JI instruments with a finite number of fixed notes must decide which notes to include and which to leave out. (While equal temperament is like a round Earth where if you go too far in one direction you end up back where you started, JI is more like a flat Earth where if you wander too far in any direction you'll run out of notes / fall off the edge. So, we need to stake out enough territory to satisfy our musical needs.) Small number ratios are generally more useful than large number ratios and a certain set of small number ratios can be used to construct a familiar chromatic scale. So, those at least are fairly obvious to include. Some others are useful in some musical contexts and not in others. How many of those others to include and which ones is a difficult design choice that affects what sort of music can be played on the instrument.
Guitars have practical limits on the density of frets; too few frets and they aren't very versatile, capable of playing only certain songs. Too many frets, and chords become physically impossible to play correctly.
A related problem is that there are practical limits to how close any two frets can be to each other. In just intonation, it is sometimes useful and necessary to have multiple notes that are almost but not quite the same pitch, which may not allow adequate space for a finger to press down without muting the string somewhat.

a just intonation guitar (key of A) with a fingerboard that's a bit too crowded


another JI guitar (key of G) with a less crowded fingerboard
In addition to choosing a scale of notes, it is also necessary to choose a key. In most cases, a different tonic root will require either a different fingerboard layout or a major change in string gauge and/or tension. (Sometimes it's possible for a JI guitar to be usable in several adjacent keys.)
So, while guitars do make very good JI instruments, they tend not to be very versatile due to the limited number of scale notes that can practically fit on a fingerboard. In order to play in different keys or use different scales, it is necessary to own multiple guitars, each one designed for a specific purpose. Trying to make a guitar that's capable of playing anything results in a guitar that is just too hard to play to be useful.
The piano is another fixed-pitch instrument that I enjoy playing, so that led me to consider how JI would apply to a keyboard-type instrument.
The piano interface is so ubiquitous, it's hard to imagine a keyboard designed any other way. So, the obvious first choice would be to simply re-tune a piano or keyboard for JI.
Re-tuning a piano is a laborious process (though the results can be rewarding for those who go that route). Re-tuning an electronic keyboard is at least in theory easier, but even that turns out to be trickier than one might expect due to the limitations of MIDI (more on that later).
Supposing that tuning the piano were not a problem, there are some other limitations to consider. For instance, the arrangement of white and black keys strongly suggests the use of a 12-note scale. Attempting to use any number of notes per octave that isn't evenly divisible by 12 wouldn't align with the pattern of white and black keys, and so remembering what key corresponds to which note would be needlessly difficult.
In JI, being restricted to a 12-note-per-octave scale is very limiting. As with guitars, it would be necessary to use different layout for different songs and switch between them. Not impossible, but it would be difficult to learn any one layout well when constantly switching (like going back and forth between qwerty and dvorak). A 24-note-per-octave layout is a more versatile option, but my fingers are nowhere near long enough to span a 24-note octave.
Another limitation of most keyboards that isn't related to tuning but that I'd like to address anyways is that they don't provide much control of the volume of a note over time. Electronic keyboards are typically designed with a double switch mechanism that only measures the initial velocity of the key strike and sustains until the key is released (like a mechanical piano). This does not give the performer a way to do volume swells or add a tremolo effect by varying key pressure over time. (Actually, there are some keyboards that support "aftertouch" as it's called, but they're either expensive or they only support whole-channel aftertouch. I've never used a keyboard with polyphonic aftertouch, but from some experiments sending aftertouch commands to a Roland XV-2020, it appears that the Roland uses aftertouch as an expression control, not for volume.)
This got me thinking: suppose one were to construct a keyboard designed for just intonation... what would it look like?
I decided on the following design constraints:
Where do these design constraints leave us?
Having more notes per octave without increasing the width that fingers must stretch to span an octave implies that we need to either make the keys narrower, or arrange them in two dimensions like a typewriter.
A two dimensional layout seemed like a more attractive option, but how exactly should the keys be arranged? The simplest thing would be to use a regular rectalinear or hex grid. The problem with a regular grid, though, is that there isn't an easy way to choose where each note goes that won't lead to weird inconsistencies or unused spaces or require major re-arrangements to the keyboard if I change which notes I want in my scale. I would like to be able to decide whether or not to include, say, a 7/5 note without having to shove a bunch of other things out of the way to make room for it.
One kind of regular grid used occasionally by musicians is a lattice. Musical lattices are a useful abstraction for describing the relation that notes have to each other. Typically, a 2-dimensional lattice is used with the horizontal axis corresponding to movement in perfect fifths, and the vertical axis corresponding to major thirds. Octaves would theoretically exist in a third dimension, but they're usually ignored. (Lattices are usually used to analyze harmony, in which octaves aren't terribly important.)
In just intonation, we can think of moving right and left in fifths as multiplying or dividing by powers of three, and moving up and down by major thirds as multiplying or dividing by powers of five.
| 100:81 | 50:27 | 25:18 | 25:24 | 25:16 | 75:64 | 225:128 | 675:512 | 2025:1024 |
| 160:81 | 40:27 | 10:9 | 5:3 | 5:4 | 15:8 | 45:32 | 135:128 | 405:256 |
| 128:81 | 32:27 | 16:9 | 4:3 | 1:1 | 3:2 | 9:8 | 27:16 | 81:64 |
| 512:405 | 256:135 | 64:45 | 16:15 | 8:5 | 6:5 | 9:5 | 27:20 | 81:80 |
| 2048:2025 | 1024:675 | 256:225 | 128:75 | 32:25 | 48:25 | 36:25 | 27:25 | 81:50 |
JI lattices have some interesting properties. Every ratio that can be constructed from powers of three and five has a unique position on the lattice. Every type of chord has a distinct "shape" that is the same regardless of where it appears in the lattice. left-leaning, upward pointing triangles are major triads. Right-leaning, downward pointing triangles are minor triads. Squares are major7 chords. A chord that has three notes in a row has an added ninth, and so on.
Similarly, to transpose an sequence of notes that make up a song to a different key, we can just move that pattern over to start on a different note. The relative movement is the same, it's just displaced.
I recently stumbled across some great videos on YouTube by Gary Garrett demonstrating how a lattice works. Here is one:
Flying Dream by Gary Garrett. (Lattice leans to the right to form triangles; notes labeled according to the Nashville number system.)
Another good lattice example is this one taken from W.A. Mathieu's book Harmonic Experience.
In just intonation, it's useful to talk about prime limit. The prime limit of a scale is the largest prime number that occurs in the factorization of all of the notes in the scale. Ancient music based on Pythagorean tuning had a prime limit of 3. Most modern "normal" music has a prime limit of five, meaning that all the notes can be constructed from some combination of powers of two, three, or five. (Ben Johnston refers to this as "triadic just intonation".) However, we don't have to stop at five. Sevens are used by barbershop quartets to construct dominant seventh chords in which the individual notes have a 4:5:6:7 relationship to each other. (It's a notational coincidence that 7/4 can serve as a "minor seventh", or the seventh note of the major scale flatted.) Outside of barbershop dominant sevenths, 7-limit notes can sound very unfamiliar and yet still seem musical in the right context. Larger primes like 11 or 13 are mostly unexplored territory.
As an abstract concept, lattices extend to infinity and may have as many dimensions as the number of prime factors we care to consider. An actual keyboard has a limited number of keys, and is confined to no more than two dimesions, so in order to use a lattice directly as a keyboard layout, we must select some subset of notes in our scale and then project that subset of our many-dimensional lattice onto two dimensions.
(It's also worth pointing out that while lattices are particularly convenient for describing harmonic relationships, they aren't the only method of organizing the rational numbers. Calkin-Wilf trees and Stern-Brocot trees are interesting alternatives. It isn't obvious to me how one would arrange them into a usable keyboard layout that would make sense to a musician, but perhaps there's a non-obvious solution.))
A lattice projected onto a plane has a certain regularity to it, but it isn't quite the same as a regular grid, so we need some way of dealing with irregularly spaced keys in a way that will fit together properly. A standard way of dividing a surface into irregular polygons centered around some arbitrary points is a Voronoi diagram. A Voronoi diagram begins with some chosen "seed" points, and around each point is a cell. Any point which is closer to a particular seed point than any other is within that seed point's cell. The resulting cells have polygonal shapes that resemble the way soap bubbles rest against each other. Voronoi cells are always convex but they can be different sizes (especially if the seed points aren't evenly spaced).
There are efficient algorithms for generating Voronoi diagrams, but since the efficient solutions are complicated and the number of points I will be dealing with is relatively small, I chose not to concern myself over-much with computational complexity as long as it isn't absolutely terrible.
The easiest way I could think of was to generate the Voronoi diagram from a Delaunay triangulation (that conversion is pretty straightforward), and to generate the Delaunay triangulation by considering all possible lines between any two seed points, and then consider all pairs of such lines. If line pairs cross, then remove the longest line. All the lines that remain are part of the Delaunay triangulation.
My initial attempt at the algorithm was, I believe, something like O(N^8). That's pretty bad, and it took longer than I'd like to compute a solution. I added a heuristic to remove lines that are longer than some threshold and made some data structure tweaks, but it was still annoyingly slow.
My implementation is written in Haskell. I had been executing my program from the ghci interactive shell (the so-called Read-Evaluate-Print-Loop, or REPL). Ghci is able to reload quickly when I make a source change, but it doesn't run very fast. On the other hand, I can compile an efficient binary with the the compiler, ghc. Ghc runs slowly, but it emits pretty good code. So, by compiling a proper binary and running it I was able to get a pretty big improvement. I was then spending about twice as much time waiting for the compiler to run after each change as it took to do the actual computation, but overall it was a significant improment over trying to do the calculation within the slow-ish REPL. I believe there are Voronoi diagram solvers that run in NlogN, which would be practically instantaneous even for thousands or millions of points, but what I had was good enough so I moved on to other problems. (Sometimes it's nice to live in an era of fast computers.)
An additional tweak to my voronoi diagram solver was, in order to mimic the long, narrow keys of a piano (which seemed desirable for ergonomic reasons as well as aesthetic), I adjusted the algorithm to produce voronoi cells that are stretched vertically.
I imagined the project progressing in three stages:
With a voronoi diagram solver, that meant I could get started designing and building the keybed. The other two tasks seemed pretty daunting, so I ignored them till later.
My first major decision was what notes to include and what notes to leave out. I started off with the seven notes of the major scale: 1/1, 9/8, 5/4, 4/3, 3/2, 5/3, and 15/8. Sometimes I also like to consider 10:9 to belong to the major scale, but for my purposes I left it out for now.
Next step was to consider all the notes reachable from any of the major scale notes by going up or down by a fifth, a major third, or a minor third. Basically, we expanded our lattice by one step in all directions, which brings us up to twenty notes (including the 10/9 I left out in the previous step). In addition, I added all the notes reachable by going up from any of the major scale notes by the interval 7:4. This gives me some seven limit intervals to play with, and brings the tally up to twenty-seven.
One kind of tuning system (employed by Ben Johnston's Suite for Microtonal Piano) uses only notes from the harmonic series. Johnston used the 16th through the 32nd harmonic, skipping a few so that he could fit the notes into a 12-note-per-octave piano scale. Following his example, I added in 11/8, 13/8, 17/16, and 19/16. That brings our tally to 31 notes. That's less than Harry Partch's 43-tone scale, but as long as we aren't trying to play 11-limit music, it should suffice for most purposes.
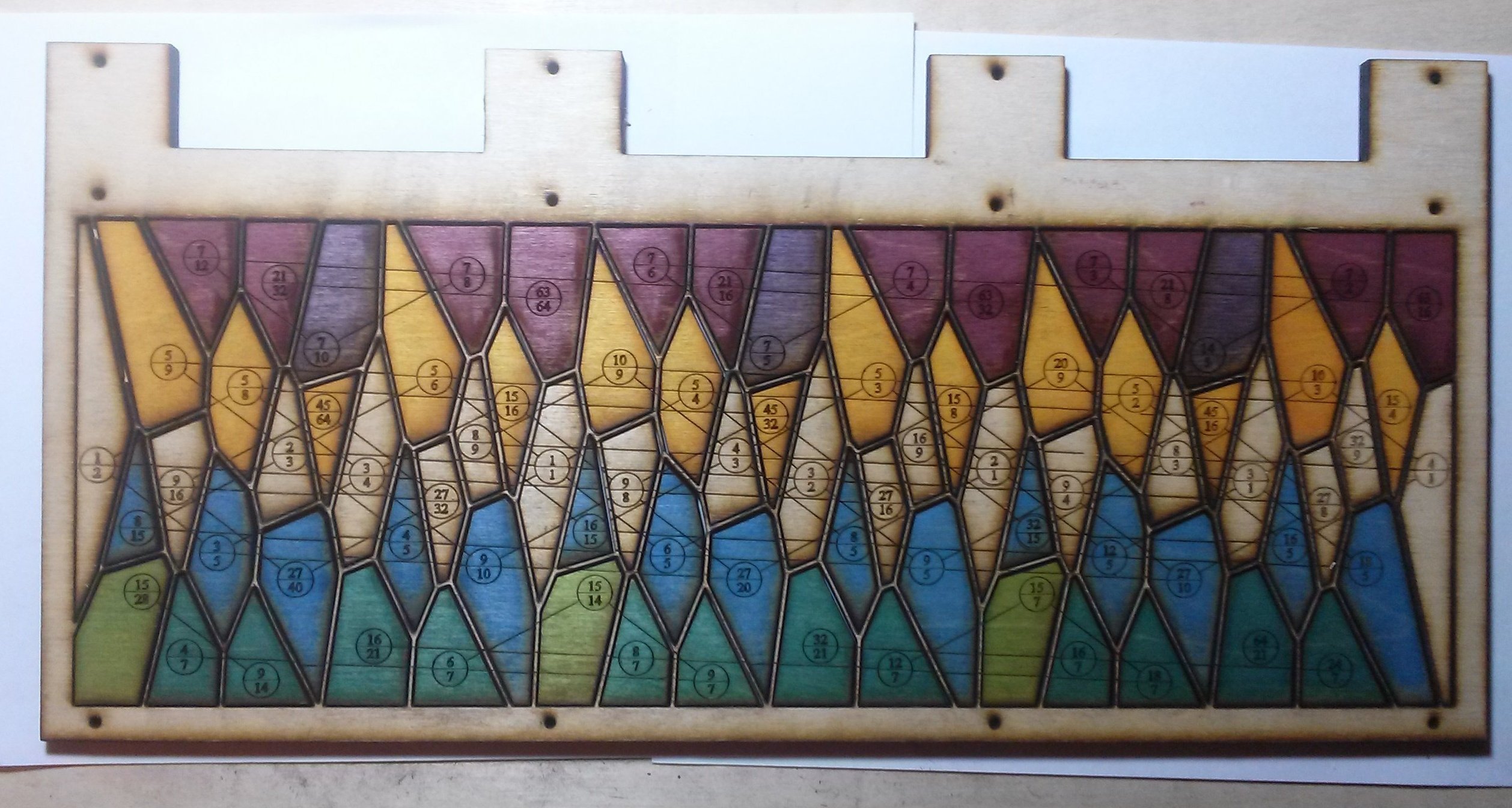
My 31 note scale in the key of C, with some of the familiar notes and chords labelled.
Our scale thus far, in order of increasing pitch and labeled more-or-less according to Wikipedia's list of pitch intervals:
31 is a nice place to stop. I wanted to limit the design to a nice power of two notes per octave to make it easier on myself when I built the electronics, but I also wanted the highest and lowest note on the keyboard to be an octave-shifted version of 1/1, which meant that somewhere I would have to add a key twice to avoid committing a fencepost error. (Most smaller piano-style keyboards adhere to a similar pattern, so that the top and bottom note can be C; typically the number of keys will be (12 times N) + 1, for some N. So, 25, 49, and 61 keys are common.) The easiest solution was to just limit myself to 31, so that one octave can have the full 32.
There are some notes my scale lacks that would be nice to have, like 7/5, 10/7, and 14/9. Perhaps next design I will add those and make do without the 25's and the 35's, which I haven't found a lot of use for thus far.
There's a trick I used to convert the notes of my scale into seed points for my voronoi diagram solver. Firstly, the absolute pitch of the note determines its location on the horizontal axis. (This shouldn't be surprising; piano notes get higher going to the right and lower going to the left.) I found it convenient to calculate pitch in cents, with 1200 cents corresponding to the width of an octave. (Cents is a log scale.)
The vertical placement is a bit more complicated. I broke the ratios into their prime factors and then applied some fixed offset for each prime, with primes in the lower part of the fraction given the opposite offset.
For example, the offset for factors of 2 is zero. This means that notes that are an octave apart line up horizontally.
The offset for powers of three is a small negative number. This means that fifths slope down to the right. Powers of five have a large positive offset, which means major thirds slant steeply up to the right.
I wanted powers of 7 to be up and out of the way (since I don't intend to use them as often as the 3 and 5-limit intervals), so I gave 7 a very large offset.
I only had one 11, 13, 17, and 19-limit note, so basically I just applied whatever offset that would place it somewhere it wouldn't get in the way of anything else.
Through trial-and-error, I came up with a set of prime offsets that didn't have any notes that were too close to each other.
For the sake of ease-of-use, I incorporated into the design some engraved lines to identify perfect fifth and major third relationships between notes. (Even though going up or down by a third or a fifth, or any other musical interval at all will always be in the same direction and the same distance, The keyboard is cluttered enough that it's hard to see patterns without some help.)
I decided to give my keyboard a five-octave range. That's less than the 7-octaves-and-a-minor-third range of a piano, but still respectable. It's the same range as a 61-key standard keyboard, but since I have 31 notes per octave that leaves me with 156 keys. That's enough to give me a strong incentive to find cheap, easy construction techniques. If I need a lot of effort or money or bulky components per key, this isn't going to work out.
The result was this keybed more-or-less ready to be built:
5-octave keyboard layout.
About the same time I started working on this project, I ordered a 45 watt CO2 laser cutter from Full Spectrum. (It's their Hobby Laser model.) It looks like this:

liven up your dining room with the pleasant pink glow of plasma
The laser cutter has a work area of about 20" by 12", and can cut through quite a few different materials. For the purposes of this project, it's important that it can cut through 1/8" and 1/4" birch plywood and cork (though the latter smokes a lot, and I don't really recommend it if you can think of a better option).
(For those curious about laser cutters in general, I will add that it's pretty low maintenance once you get it set up and calibrated. The software has some weird quirks but it does what it needs to do. The machine with the options I ordered, including upgraded 45 watt laser tube, cost about $4200. It requires external exhaust or an expensive air filter, a bucket of distilled water for cooling, and uses a small air compressor to blow smoke out of the path of the beam. I would recommend this same machine for anyone who wants to do the kind of stuff that I'm describing here. I don't know how I could have built this keyboard without a laser cutter.)
The keybed is actually kind of complicated. The design I came up with eventually is that the keys themselves would be 1/4" plywood backed by cork. The cork gives the keys a bit of a squishy feel, so it doesn't feel like I'm pressing on an absolutely immovable block of wood.
The back of the keybed is a thick piece of plywood the size of the whole keyboard, which gives it its structural rigidity.
In between the keys is a thin framework that holds the keys in place and prevents them from falling out. How this is accomplished is that the cork on the bottoms of the keys is cut slightly bigger than the keys themselves. The framework between the keys is printed in two 1/8" thick layers; the top-layer frame has thicker walls than the bottom-layer. This provides a tiny lip to catch the edge of the cork, which means I can turn the keyboard upside-down without all the keys falling out. (This is very important.) However, the difference isn't so great that I can't pull the keys out and put them back in easily.
The full five octaves is too wide to cut out in the laser cutter in one pass, so I have to split up the work and print a set of left-hand parts then a set of right-hand parts. Which means I spend a lot of time in Inkscape deleting half the keyboard, cutting, then deleteing the other half and cutting. Kind of aggravating, but not a big deal in the long run.
some assembly required
When you add it up, theres a lot of cutting to be done. There's the 1/4" key tops, the cork key bottoms, the upper and lower layer of the keybed frame and all of those have to be cut out as two separate jobs, since the laser cutter just isn't wide enough to do it at once. So, that's ten cutting jobs. Each one takes about an hour or so plus some time doing setup work and fiddling with the SVGs in inkscape, so that's a full weekend project just to do the cutting (assuming nothing goes wrong). The birch ply costs less than a dollar a square foot at my local supplier (which is Crosscut) if I buy it in 5' by 5' squares and the cork isn't particularly expensive either, so that's about $15-20 in material costs, plus maybe $10 or so for the big thick plywood rectangle that I use as the back, and a few dollars worth of screws. Not bad.
The final result of months of design and planning and work was a very attractive keyboard-like inanimate object that doesn't do anything at all. For about six months, the project sat in that state while I considered how to go about building the electronics.
A rational course of action at this point would have been to learn KiCad, design a proper circuit board, send it to Osh Park, and have them send me back my board that I can then solder all my components to and have a robust, reliable, professional-looking device. I didn't do that. The main reason was that I would need a circuit board that extended all the way under the keybed to make electrical contact with pressure sensors. That's a very simple layout, but my project has a lot of surface area. Osh Park's cheapest option runs a dollar a square inch if you buy 10 copies of a design. So, I could design a single-octave board and order ten of them, enough to do two five-octave keyboards. That's pretty expensive. So, I wanted a cheaper option for the large underside of the keybed at least.
CNC routers are pretty good at making simple, single-layer circuit boards like I would need. I could probably have arranged for a local maker space to cut me out some. In the end, though, I went with a more primitive solution, using the tools I had at hand -- mainly the laser cutter.
suddenly, a new folk art
My solution was to make my circuit boards out of plywood. By lasering a groove of the right depth and width, I was able to create channels to press copper wires into and glue in place. Beneath each key, I wanted to have an electrical contact; this I made by painting a circle of conductive paint in the appropriate spots at the end of each trace. I then painted over the exposed copper with polyurethane. I'm not sure if that's the optimal insulator to use, but it seems to work.
One of the neat things about doing it this way is that the ends of the traces can be trimmed to the appropriate length and then jammed into a solderless breadboard. No need to contrive some sort of connector. (Somehow, I managed to do this whole project without soldering a single thing. I'm not sure if that's something to be proud of, but I am.)
At around this point it became obvious that my original keybed wasn't big enough to fit the electronics I wanted to add, so I made a larger base. Once again, this was made of plywood. I used a router to make a recess up top so that I wouldn't have random stuff sticking up quite so high. I used copper tape with conductive adhesive as a ground plane. (I live next to a light rail line, so I tend to be a bit paranoid about shielding everything I can from 60-cycle hum.)
bigger key bed with room for breadboards
I purchased a number of solderless breadboards to accomodate the chips I would need with some extra space left over for whatever buttons and LEDs I want to add later, cut some of them to a more convenient length, and then attached them with double-sided tape. I left room at the upper left for a Raspberry Pi and its various connectors.
one hundred and fifty-six electrical contacts exposed
So, how does this whole pressure sensor thing work, anyways? Well, over the "circuit boards" with their electrical contacts that make up the bottom layer is a layer of a film that has the interesting property that applying pressure causes its electrical resistance to drop significantly. This stuff comes in 11" squares, so unfortunately it's not possible to just use one big sheet. One sheet covers two octaves, so I had to use two and a half sheets. (Originally, I used two layers but later changed my mind and reduced that to a single layer.)
It's worth noting that I purchased a huge roll of Velostat hoping it would perform the same as the stuff Adafruit sells, and I could use a single large sheet across the whole keybed and not have any seams. Unfortunately, it doesn't seem to have the same electrical properties and I'm not sure if it's at all usable as a pressure sensor.
Adafruit also sells this stuff, which is more expensive than their other film and is only available in smaller squares, but it seems to be more responsive. Its resistance is also a lot higher, which in general is good because it means less current wasted, but the MCP3008s aren't designed for high-impedence outputs, so they might need a buffer. I might give it a try if I build a version 2.
On top of the pressure film goes a layer of plain ordinary aluminum foil, which is connected to ground.
At the other end of our electrical circuit, the electrical contact under each key is connected by its long copper wire to a pull-up resistor connected to a voltage source and one input of an ADC chip (basically, a digital voltmeter).
wiring diagram of a single key; increased key pressure results in lower voltage read by the ADC
The ADCs I used are MCP3008s. These are commonly used to add analog inputs to Raspberry Pi projects and are supported by Wiring Pi, so you don't have to do much work to start using them.
Each MCP3008 has eight inputs and reads ten-bit values (0 to 1023). MIDI volume is only 7 bits, so that gives us three extra bits of precision. We need 4 MCP3008s per octave, or 20 in total in order to construct what is basically a 160 channel digital voltmeter. A single MCP3008 is not quite four dollars, so twenty of them make up the most expensive part of the keyboard.
Connecting twenty MCP3008s to a single RPi was the most difficult electronics problem I had in building the keyboard.
The MCP3008 communicates over a SPI bus. SPI busses are fairly simple; they have a clock wire, a master-out-slave-in wire, a master-in-slave-out wire, and a slave select wire.
It's that slave select wire that's a problem. We can daisy-chain as many MCP3008s as we want on one big long bus, but in order to use any of the devices we need to ensure that only one is enabled at a time. If more than one is enabled, they'll both try to send data at once and we'll have data corruption.
The most straightforward thing would be to run twenty wires from the RPi, one to the chip-enable pin on each MCP3008. This could work, but it consumes a lot of pins. The RPi does have a lot of pins to spare, but we might want to use them for something else. Better to find a more pin-efficient solution.
This seemed like a great application of a shift register. A shift register has an input and a clock pin, and stores some bits which are sent to output pins. When the clock ticks over, the shift register reads the input to determine the new value for its first bit, and shifts the rest of the bits over by one. Shift registers can be chained, so with three 8-bit shift registers, we can accomodate our 20 MCP3008s. We just need to set the shift register to activate the first MCP3008, read its values, cycle the clock which will enable the next MCP3008, and so on.
This all sounded simple and elegant. It also doesn't work, because of one of the MCP3008's strange little quirks. Apparently, in order to read all eight values from an MCP3008, it is necessary to read the first value, disable the chip, re-enable it, read the second value, disable it, re-enable it, read the third value, and so on until all the values are read. Our simple shift register scheme doesn't provide us with a way to toggle the enable bit on and off without shifting.
The solution I arrived at was to use some logical gates to combine the output of the shift register with the RPi's hardware slave select line. So, we can toggle the slave select on and off to read successive values from a single MCP3008, then cycle the clock to select the next MCP3008 and do it again. This takes a lot more chips than I wanted, but it doesn't use very many pins. So, I guess it's a success, even though the top of my keyboard now looks like a plate of spaghetti.
I'm glad I used solderless breadboards; if this were a proper circuit board, I would have had to order multiple revisions.

tangle of wires
I used a Raspberry Pi 2 as my microcontroller. I could have used a different microcontroller, but the RPi is inexpensive and seemed to be the best option for what I wanted to do. I wanted something with enough CPU power to run its own MIDI synthesizer, and I wanted an analog audio output. HDMI out wasn't necessary, but it's nice to have in case I come up with some cool visualization tools or I want to debug the system by using its desktop environment. (The RPi 3 came out shortly after I purchased a couple of RPi 2's. That's fine; I don't really need wireless networking for this project. In fact, it's probably better that I don't have it -- this isn't meant to be a high-security device, and I don't want it to become part of the so-called "Internet of Other People's Things". Better to use physical ethernet occasionally for debugging than have it permanently on the network.)
There were some things I had to tweak to get the RPi to work the way I needed it to. The audio output was quite terrible, but eventually I came across a workaround that required updating the firmware and some boot parameters to use a different smoothing algorithm. It sounds much better now.
Wiring Pi was able to use the MCP3008s right away, but the existing code runs the SPI bus at 1mhz. That's pretty slow, so I had to make a fork of some of the MCP3008 initialization code so that I can set higher speeds. (Ultimately, I wasn't able to go past 2mhz because at any speed past that, the ADCs start reporting weird truncated values. Apparently they need time to settle to get an accurate reading. There may be a workaround I'm not aware of. At 2mhz, I'm able sample the whole keyboard about 90 times a second. Not bad, but there's room for improvement.
For a MIDI interface, I just use a usb-to-midi adapter. When I plug it in, it shows up on the RPi as /dev/midi1, and I can write raw bytes of MIDI data to it like any file. In order to use Fluidsynth as a local MIDI synth, I plug the usb-midi adapter's output plug into its input plug using a MIDI cable coupler. There ought to be a way to do this purely in software and not have to route all my MIDI packets over a 31.25kbps serial interface, but I haven't figure out how.
One might expect that electronic synthesizers would be well suited to microtonal music. The choice to use a twelve-tone equal temperamered scale or not, after all, is simply an arbitrary implementation choice; one could imagine re-tuning the notes of a synthesizer's scale simply by adjusting some oscillators or changing some numbers that are hard-coded in software. Sadly, most synths are not designed with anything other than 12-TET in mind. Most that provide alternate tuning tables only provide a few non-editable presets of historical tunings or whatever else the developers thought was important at the time, or they only provide a 12-note-repeating-octave scale (i.e. too few notes to be of much use for JI), or both. The disinterest of synth manufacturers in JI is compounded by the limitations built into the MIDI protocol that those manufacturers have used since the 80's to make sure their products interoperate with those of their competitors. This was a noble goal, and it works great as long as your instrument is an electronic piano. Instruments that aren't and don't function like pianos have a harder time. For instance, MIDI is limited to 128 notes per channel (which is not enough for my keyboard) and it doesn't have a widely-supported way to adjust the volume of an individual note over time. (Polyphonic aftertouch could be used for that, but the rare synths that support it seem to prefer to use it to add vibrato or whatever rather than as a means to control volume.)
One of my (unrealized) goals when I began this project was to write my own synthesizer. I could create a new MIDI-like protocol without MIDI's limitations for my keyboard to use, and then, since there aren't any available synths to speak this new protocol, I would make one.
I got as far as designing my ideal protocol and writing some code to read and write some of the commands. However, as soon as I had the electronics of the keyboard working, I wanted some quick and easy way to test it out. So, I figured I'd try using MIDI as a temporary solution. It turned out to work better than I expected, so that's what I've been using. I still think MIDI ought to be replaced by something better and I have strong opinions about what that "something better" ought to look like, but that's a problem I don't need to solve right now.
MIDI doesn't really have a widely supported standard way of dealing with custom tuning systems. (There's something called the MIDI tuning standard, but I think it's only supported by a handful of synths.)
Some synths do have ways to configure tuning tables, though. The Emu Proteus 2000 (which I have on hand) is very nice in this respect in that it doesn't assume a 12-note scale of repeating octaves; every MIDI note can be tuned indepenedently of the others, in increments of a 64th of a semitone. (That's about one and a half cents; not ideal, but probably too small to notice.) Still, I would need to use mulitple channels to support the full 156 notes with a static table.
I wanted my keyboard to work with other synths besides the Proteus, and I also wanted the ability to adjust the volume of individual notes over time in response to key pressure, something that no synth I owned seemed capable of doing. It turns out that both these problems have a common solution.
Several years ago, before I began this project, I attended a meetup in Portland and learned of a way force synthesizers into arbitrary tunings using only a handful of widely-supported commands. At this meetup, Kite demonstrated a program he had written called Alt-tuner. Alt-tuner intercepts MIDI commands from a standard keyboard and translates them into different MIDI commands that use multiple channels and pitch bend to force notes into the desired tuning. Alt-tuner has some other interesting features as well, like visualization tools and the ability to switch layouts on the fly.
Alt-tuner is designed to work with the kind of MIDI events generated by normal keyboards. However, my keyboard is pretty strange and needs to do non-standard things like spread the notes across multiple MIDI channels and send continuous key volume updates. Getting it to work with Alt-tuner didn't seem any easier than just generating MIDI data directly similarly to the way Alt-tuner does it, so I did the latter.
It works like this: The MIDI protocol has 16 channels. Typically, one would use multiple channels to connect multiple instruments to a single synthesizer. That way, each instrument can do its own thing without interfering with the others. MIDI also has a pitch-bend command that tells the synth to "bend" the pitch of the whole channel up or down by some amount. (The pitch bend value is 14 bits.) What constitutes a full pitch bend is up to the synth. Typically, a full bend would be either an equal-tempered semitone, a whole tone (two semitones), or an octave (12 semitones). If we know what the synth considers a full bend to be, we can play an exactly-tuned note by picking the nearest equal-tempered note and using the pitch bend command to tune the whole channel up or down before we send a note-on command.
We might want to play multiple notes at the same time. Since pitch bend affects the whole channel, we need to play each note on a separate channel.
An exception to this is notes an octave apart; those could be played on the same channel because an equal-tempered octave is the same as a JI octave. So, we can support up to 16 separate "pitch classes" by assigning a separate channel for each pitch class. Unfortunately, that doesn't work in my case because my 31-note-per-octave scale has 31 pitch classes. So, instead of statically assigning a channel to each pitch class, I'll have to allocate channels dynamically.
Dynamic channel allocation is pretty straightforward. Whenever you begin to play a note, your program checks if any channel is currently allocated to that note. If not, it finds the least-recently-used channel, sends a note-off command to stop whatever note is playing on that channel (if any), pitch bends it as appropriate, and sends the proper note-on command.
It turns out that there's a standard way of adjusting the volume on a per-channel basis as well, through control change command 7 (channel volume). Control change 11 (expression) also seems to work on most synths. The way I do dynamic volume is that I always use the same fixed initial velocity in every note-on command, but I adjust the channel volume up and down based on key pressure. This allows me to do volume swells whenever I please. (On some synths, setting the channel volume to zero may kill the reverb as well. Using an external reverb after the MIDI synth fixes this, but it's kind of a cumbersome solution. Another sort-of fix is to only allow volume to decay at some fixed maximum rate.)
Channel volume is also incompatible with the idea of allowing multiple notes that are octaves apart to coexist on the same channel, but that's okay; dynamic channel allocation allows us to play up to 16 notes at a time, which is plenty.
I've considered sending the initial key pressure as the note-on velocity, instead of using only one fixed velocity for every note. (Some instruments have a different timbre depending on velocity, and it seems like a shame to loose that feature.) I haven't tried it yet, but if I do I may need to delay sending the note-on until I've gotten at least two samples from the ADC, since the first might not be accurate (it might only have been sensing pressure for part of the sampling time). If I do this, it'll be some kind of "piano mode" I can turn on and off.
So far, I've gotten several synthesizers to work well with my keyboard. The simplest setup is to use the open-source FluidSynth running on the Raspberry Pi. Sound quality isn't particularly amazing, but it's kind of nice to be able to plug in a USB battery pack and headphones or USB-powered speakers and be able to play the keyboard sitting on a couch or wherever and not have to be plugged into anything.
I use my EMU Proteus 2000 most of the time when I want pretty good quality sound. It's kind of old and sounds a little dated, but it's a well designed and easy to use synth with some interesting features like flexible tuning tables and a second MIDI in port for twice as many channels. There's also a master effects setting that can be used to enable reverb in a way that isn't affected by channel volume.
The Yamaha MOX 8 works quite well. Reverb is not affected by channel volume, so I don't need to use an external reverb unit. I did have to do a factory reset since for some reason certain channels were octave shifted. It also is a little slow to respond to bank select commands.
The Roland RD-300NX works well and sounds great.
The Roland XV-2020 took awhile to get it to work smoothly; apparently, it doesn't respond to control change 7 (channel volume) fast enough to play smoothly, but CC 11 (expression) basically does the same thing and it responds to that command much quicker.
The Roland AX-Synth only works as a monophonic synth, as it is only able to listen to one MIDI channel at a time. (It isn't a multi-timbral synth.)
Analog synths generally have the same limitation as the AX-Synth; they only receive on a single channel at a time, which means for my purposes they're essentially monophonic. Many analog synths are monophonic by design, though, so clearly there's a use for such instruments. I've done a little bit of experimentation with a Moog Slim Phatty. I had to make some software changes on the keyboard to prevent it from oscillate back and forth between two notes if I happened to be pressing two keys at once. (It is kind of an interesting effect, though.) The Moog seems like it would be a good option for a bass part or a solo.
I haven't tried any software VSTs, though I may at some point try and see if Hauptwerk supports multi-channel MIDI.
It's worth noting that the channel-per-note strategy is used by some other instruments, such as the Linnstrument. The Roland GR-55 guitar synth has a mode where it uses a separate channel for each of the six guitar strings. I'm not aware of any other channel-per-note instruments besides my own that use control change 7 (channel volume) or 11 (expression) for volume swells, but it wouldn't be surprising if some of them do.
Apparently, there is currently an effort to create a MIDI extension called Multidimensional Polyphonic Expression (MPE) which, if adopted, may make it easier to do channel-per-note MIDI in a standard way.
Once I had the device up and running, it took quite a bit of adjustment to get it into usable state.
My first major problem is that some of the keys activate with light pressure, some require much more pressure, and some activate when I don't press on them at all. So, there's quite a bit of variability from key to key as to how much pressure results in how much voltage.
As an example of the variability I see just while the keyboard is at rest, here is a typical set of raw pressure readings from all the keys:
(1,4) 36 (25,96) 34 (17,64) 23 (4,15) 18 (35,128) 21 (5,18) 25 (9,32) 33 (7,24) 17
(75,256) 10 (19,64) 66 (3,10) 68 (5,16) 18 (21,64) 36 (1,3) 65 (27,80) 51 (11,32) 50
(25,72) 25 (45,128) 57 (35,96) 19 (3,8) 39 (25,64) 21 (2,5) 50 (13,32) 17 (105,256) 26
(5,12) 57 (27,64) 87 (7,16) 57 (4,9) 77 (9,20) 54 (15,32) 53 (63,128) 57 none 1023
(1,2) 4 (25,48) 10 (17,32) 4 (8,15) 9 (35,64) 25 (5,9) 4 (9,16) 4 (7,12) 69
(75,128) 4 (19,32) 4 (3,5) 10 (5,8) 4 (21,32) 4 (2,3) 9 (27,40) 6 (11,16) 4
(25,36) 3 (45,64) 4 (35,48) 2 (3,4) 4 (25,32) 58 (4,5) 4 (13,16) 4 (105,128) 4
(5,6) 2 (27,32) 4 (7,8) 5 (8,9) 94 (9,10) 9 (15,16) 4 (63,64) 4 none 1023
(1,1) 9 (25,24) 6 (17,16) 4 (16,15) 52 (35,32) 9 (10,9) 4 (9,8) 4 (7,6) 5
(75,64) 8 (19,16) 4 (6,5) 10 (5,4) 4 (21,16) 4 (4,3) 4 (27,20) 39 (11,8) 5
(25,18) 3 (45,32) 10 (35,24) 5 (3,2) 18 (25,16) 4 (8,5) 6 (13,8) 4 (105,64) 7
(5,3) 11 (27,16) 17 (7,4) 2 (16,9) 3 (9,5) 5 (15,8) 28 (63,32) 10 none 1021
(2,1) 9 (25,12) 38 (17,8) 3 (32,15) 4 (35,16) 4 (20,9) 4 (9,4) 4 (7,3) 6
(75,32) 9 (19,8) 4 (12,5) 5 (5,2) 6 (21,8) 4 (8,3) 4 (27,10) 4 (11,4) 5
(25,9) 4 (45,16) 4 (35,12) 4 (3,1) 2 (25,8) 4 (16,5) 5 (13,4) 2 (105,32) 9
(10,3) 2 (27,8) 6 (7,2) 39 (32,9) 4 (18,5) 4 (15,4) 62 (63,16) 4 none 1023
(4,1) 5 (25,6) 6 (17,4) 5 (64,15) 4 (35,8) 7 (40,9) 6 (9,2) 4 (14,3) 43
(75,16) 11 (19,4) 4 (24,5) 4 (5,1) 4 (21,4) 5 (16,3) 4 (27,5) 27 (11,2) 22
(50,9) 8 (45,8) 14 (35,6) 6 (6,1) 10 (25,4) 5 (32,5) 12 (13,2) 8 (105,16) 4
(20,3) 4 (27,4) 6 (7,1) 4 (64,9) 4 (36,5) 9 (15,2) 9 (63,8) 7 (8,1) 4
(These readings were taken after much debugging; early on, results were much more variable. Occasionally, one key's maximum pressure value would be less than some other key's resting state.)
I took the keybed apart, inspected the circuit boards, didn't find anything amiss. I put it all back together (more carefully than the first time) and still it worked about the same.
So, possibly there are bad electrical connections somewhere, or my pressure resistive film is not uniform and has patches of high and low resistance, or maybe the key pressure isn't being transmitted quite uniformly. On a whim, I tried placing a small piece of electrical tape on the alluminum foil underneath one of the poorly-responding keys right on top of where the electrical contact is. The result was a significant improvement in the responsiveness of that key. So, at least for some of the keys it seems that the problem is one of key pressure. Perhaps the cork isn't uniform enough, and has hard or soft spots?
At any rate, adding a small electrical tape shim fixed most of the problematic low-response keys. For the ones that activate when I don't want them to, I created a per-key minimum activation threshold value and a maximum pressure threshold value. For awhile, I set those manually by editing the C file.
That sort of worked and after awhile I had fixed most of the problem keys so I didn't get stuck notes very often. However, I still had quite a bit more pressure variablity between keys than I liked. I decided I needed some sort of formal calibration procedure.
I modified my ADC-scanning program to record the maximum pressure value ever recorded for each key, and after some time period to dump those out as a C header file that can be compiled with the program. (I probably should have just used a data file, but who can resist having a program dynamically re-write itself?)
I set the min threshold by running the program once and manually pressing all of the keys with very light pressure. For the max threshold, I did the same thing but applying more pressure to each key.
The end result wasn't perfect (I still spent a couple weeks fixing whatever the stuck-note-of-the-day happened to be), but eventually I stopped seeing stuck notes very often and the keyboard is much easier to play.
Something I was worried about is whether pressing a key will cause adjacent keys to trigger, since the velostat is somewhat conductive and the keys aren't really isolated from each other. This does happen sometimes, but so far I've been able to work around problem keys by adjusting their activation thresholds.
One change I would make (and I probably will eventually, but it would require taking the keybed apart again) is to make the electrical contacts beneath the keys bigger. Right now, the key really only responds if you press it exactly dead center. Maybe that's good for learning to play accurately, but ergonomically it would be nicer if it was more forgiving and I didn't have to contort my fingers quite as much to play chords.
I added a couple of microswitches to toggle up and down through the voices of one particular bank of voices. Changing voices sends the appropriate command on all 16 channels. I also have a similar way of cycling through bank select LSBs and MSBs to access different sets of tones. There are some other settings I'd like to be configurable directly from the keyboard without resorting to editing C files over ssh, such as the ability to change the master tuning (i.e. switch keys) and to octave shift the keyboard up and down.
I've also been experimenting with using an M-Audio Trigger Finger to control my keyboard, since it isn't very bulky and it has a lot of knobs and sliders that I can assign to different control change parameters. My keyboard can either act on CC messages it receives, or it can re-transmit them on all 16 MIDI channels. This gives me an easy way to control a synth without having to laboriously duplicate my settings 16 times.
I can use a similar trick with the Proteus 2000. It has some knobs on the front panel to edit various parameters of the currently-loaded patch, but normally they only update the currently selected channel. Those same settings can also be set by CC commands, and the Proteus can be configured to send those same CC messages on its MIDI out port. So, by turning that on and plugging the Proteus' MIDI out port back into my keyboard's MIDI in, I can broadcast those CC messages back to the Proteus on all channels. So, with this set up correctly, when I turn a knob on the front panel of the Proteus, it replicates that setting across all channels in real time, which is very handy.
Another usability enhancement I might do at some point is to color-code the key tops according to their prime factors. I gave this a try on a set of keys I cut out for a prototype of a 3-octave keyboard that may eventually become version 2. I used Transtint dyes thinned with water. Instead of painting the dye on, I just dropped the keys in the dye face-first and let them soak for a few minutes. It turned out pretty good:
colors by prime factors: 3-limit (neutral-sounding), 5/x (major-sounding), 7/x, x/5, x/5 (minor-sounding), x/7, 5/7
Here is a demonstration of myself playing the keyboard using an Emu Proteus 2000 as the synthesizer (set to the "Kool N Mellow" sound). Audio quality from my phone camera isn't great, but it works:
The demo consists of:
Scales: major, minor, blues, harmonic series from the lowest note up to the 22nd harmonic.
Chords: major, minor, add9, major7, a couple of dom7s.
Music: chord progression from Wagon Wheel and a million other pop songs, beginning of Pachelbel's Canon.
I also recorded another demo, this one is Doxology, with a saxaphone sound:
In both videos, the keyboard is tuned to G (i.e. the note 1/1 is 391.995 hz, and the frequency of any other note can be determined by multiplying 391.995hz by the fraction engraved on the key).
Aside from the mcp3004 files (which are from the WiringPi project and GPLv3), all this stuff above is copyrighted by myself (Jim Snow) and licenced according to version 2 of the General Public License. If you want to construct your own keyboard from these files, go right ahead.
Here are some useful books for those who are interested in this sort of thing:
There are a number of other unconventional electronic instruments out there. It would be impossible to make a complete list and I haven't actually used any of these, but here are some that seem worthy of mention (and with the exception of the Tonal Plexus which is no longer made, they are actually for sale unlike my own keyboard):
Thanks to Aaron and Kite for their invaluable advice.